`stat_tests` – Statistical tests for datasets comparisons

Introduction

The available statistical tests are:

Student’s t-test, to compare two datasets, in the student module;

The χ² test, for comparing distributions (spectra or meshes), in the chi2 module;

The Bonferroni and Holm-Bonferroni tests, to solve the problem of multiple hypothesis tests, in the bonferroni module.

Modules

`student` — Student’s t-test

In Student’s t-test, we consider 2 different datasets that can have different means and different variances. The main problem is to test if the means are equal. One way to do that is to use Student’s t-test, although technically this name should be reserved for the case where the variances are unknown but they are known to be equal (the generalized version to different variances is called Welch’s test).

In Tripoli-4, like in most Monte Carlo codes, the estimated statistical uncertainty is the standard error, i.e. the standard deviation of the mean of the samples. It is typically assumed that the distribution of the mean is normal, as a consequence of the central limit theorem. The variance of the population is estimated as

$s^2 = \frac{1}{n-1}\sum_{i=1}^n(x_i - \bar{x})^2$

and the variance of the mean is estimated as

$\bar{s}^2 = \frac{s^2}{n}$

The standard error $\bar{s}$ is the quantity that typically enters Student’s t-test.

The Student test statistic is:

$t_{\text{Student}} = \frac{\bar{x}_1 - \bar{x}_2} {\sqrt{\bar{s}_1^2 + \bar{s}_2^2}}$

Note that, with our Dataset, this is equivalent to

diff = dataset_1 - dataset_2
t(Student) = diff.value / diff.error

as value is difference of values and error is equal to the quadratic sum of the errors.

Test interpretation

The tested hypothesis in the Student’s t-test, i.e. the null hypothesis is:

equal means, so $m_1 = m_2$
Gaussian errors (or error following a normal distribution)
independent datasets.

The test interpretation is based on the comparison of the p-value with a given significance level, called $\alpha$ . The (two-sided) p-value is defined as the probability to observe results more extreme than those that were actually observed, assuming that the null hypothesis is true. Mathematically, $p=P(|X| \geq |t_{\text{Student}}|\,|N)$ , $X$ being the Student test statistic for samples of size $N$ ; the variable $N$ is also called the number of degrees of freedom. The significativity level $\alpha$ is given by the user, usually 1% or 5%. Student’s test fails if $P(|X| \geq |t_{\text{Student}}|) \leq \alpha$ . If this is the case the null hypothesis is rejected.

To evaluate the test we thus need an estimate of the number of degrees of freedom, which is typically approximated as $n_1 + n_2 - 2$ , with $n_1$ and $n_2$ being the number of batches. For large values of $n_i$ (i.e. for a large number of degrees of freedom), the distribution of the Student statistic approaches a standard normal distribution.

It is sometimes easier to evaluate if the test succeeds by directly comparing the value of $t_{\text{Student}}$ with a threshold given by the significativity level $\alpha$ and the number of degrees of freedom.

For example, here are some thresholds for some values of $\alpha$ and of the number of degrees of freedom:

	$\alpha$ = 1 %	$\alpha$ = 5 %
N = 10	2.7638	1.8125
N = 1000	2.5807	1.9623
N = $\infty$	2.5758	1.9600

Results for N = $\infty$ come from the normal distribution.

Note

This test can also be used on histograms (spectrum, mesh). In this case, an independent test is made for each bin. The test for the whole histogram succeeds if all the individual tests succeed. A better option is to use a Bonferroni or a Holm-Bonferroni test (see the bonferroni module).

Code implementation

If the number of degrees of freedom is given, p-values are estimated using Student’s t-distribution. If the number is not given or it is None, it is assumed that it is very large and the normal approximation is used.

The p-value is only calculated if the number of degrees of freedom is given; otherwise, the Student result is just compared to the threshold. To test the p-value instead of the value of the t-statistic, use TestResultStudent.test_pvalue.

All these methods use the SciPy package (see scipy). The Student distribution comes from scipy.stats.t, where the pdf is explicitely written.

The method sf of scipy.stats.t corresponds to $1 - cdf$ , so this gives the one-sided p-value; we need to multiply it by 2.0 to get the two-sided p-value. The ppf (percent point) function returns the threshold corresponding to the required one-sided significativity, so we need to divide $\alpha$ by 2.0 in our case.

The methods where the test is really applied are static methods, they can be used outside of the TestStudent class. Examples are given in the class docstrings.

Examples

Let’s get an example: one simulation gave 5.3 ± 0.2, the other one 5.25 ± 0.08. Are these numbers in agreement ?

>>> from valjean.eponine.dataset import Dataset
>>> from valjean.gavroche.stat_tests.student import TestStudent
>>> import numpy as np
>>> ds1 = Dataset(5.3, 0.2)
>>> ds2 = Dataset(5.25, 0.08)
>>> tstudent = TestStudent(ds1, ds2, name="comp",
...                        description="Comparison using Student's t-test")
>>> tstudent_res = tstudent.evaluate()
>>> print(f'{tstudent_res.tstud[0]:.7f}')
0.2321192
>>> print(f'{tstudent_res.test.threshold:.7f}')
2.5758293
>>> bool(tstudent_res)
True

To obtain the p-value, a number of degrees of freedom should be given:

>>> tstudent = TestStudent(ds1, ds2, ndf=1000, name="comp",
...                        description="Comparison using Student's t- test")
>>> tstudent_res = tstudent.evaluate()
>>> print(f'{tstudent_res.tstud[0]:.7f}')
0.2321192
>>> print(f'{tstudent_res.test.threshold:.7f}')
2.5807547
>>> bool(tstudent_res)
True
>>> print(f'{tstudent_res.pvalue[0]:.7f}')
0.8164929
>>> tstudent_res.test_pvalue()
[True]

This is also possible if we want to compare a bin to bin different spectra. Let’s define 2 small datasets containing arrays:

>>> ds3 = Dataset(np.array([5.2, 5.3, 5.25, 5.4, 5.5]),
...               np.array([0.2, 0.25, 0.1, 0.2, 0.3]))
>>> ds4 = Dataset(np.array([5.1, 5.6, 5.2, 5.3, 5.2]),
...               np.array([0.1, 0.3, 0.05, 0.4, 0.3]))
>>> tstudent = TestStudent(ds3, ds4, name="comp",
...                        description="Comparison using Student's t-test")
>>> tstudent_res = tstudent.evaluate()
>>> print(np.array2string(tstudent_res.oracles()))
[[ True  True  True  True  True]]
>>> bool(tstudent_res)
True

In the case of multiple comparisons, the test will return True if all the individual comparisons succeed. This is the case here.

It is possible to get a detailed bin-by-bin comparisons, including bad bins:

>>> ds5 = Dataset(np.array([5.1, 5.9, 5.8, 5.3, 4.5]),
...               np.array([0.1, 0.1, 0.05, 0.4, 0.1]))
>>> tstudent = TestStudent(ds3, ds5, name="comp",
...                        description="Comparison using Student's t-test")
>>> tstudent_res = tstudent.evaluate()
>>> print(f'{tstudent_res.test.threshold:.7f}')
2.5758293
>>> print(np.array2string(tstudent_res.oracles()))
[[ True  True False  True False]]

Since some of the comparisons failed here, the whole tests fails as well:

>>> bool(tstudent_res)
False

As in the scalar case, it is possible to ask for the p-values. In both cases the significativity can be changed via the alpha argument, as shown here:

>>> tstudent = TestStudent(ds3, ds5, name="comp", alpha=0.05, ndf=1000,
...                        description="Comparison using Student's t-test")
>>> tstudent_res = tstudent.evaluate()
>>> print(f'{tstudent_res.test.threshold:.7f}')
1.9623391
>>> print(np.array2string(tstudent_res.oracles()))
[[ True False False  True False]]
>>> print(f'{tstudent_res.tstud[0][1]:.7f}')
-2.2283441

This last value is in-between the thresholds at 1% and 5%, in magnitude, and therefore the test succeeds in the former case and fails in the latter.

Obtaining p-values and comparing them is also possible in the spectrum case:

>>> print(np.array2string(tstudent_res.pvalue[0],
...                       formatter={'float_kind':'{:.7e}'.format}))
[6.5481769e-01 2.6079281e-02 1.0147751e-06 8.2310894e-01 1.6125524e-03]
>>> print(np.array2string(tstudent_res.test_pvalue()[0]))
[ True False False  True False]

Finally, for an array of size 1 (and dimension 1), the test will do the same as for datasets containing numpy.generic:

>>> ds6 = Dataset(np.array([5.3]), np.array([0.2]))
>>> ds7 = Dataset(np.array([5.25]), np.array([0.08]))
>>> tstudent = TestStudent(ds6, ds7, name="comp",
...                        description="Comparison using Student's t-test")
>>> tstudent_res = tstudent.evaluate()
>>> print(np.array2string(tstudent_res.tstud[0],
...                       formatter={'float_kind':'{:.7f}'.format}))
[0.2321192]
>>> print(f'{tstudent_res.test.threshold:.7f}')
2.5758293
>>> bool(tstudent_res)
True

Like for usual operations on datasets, only tests between datasets of the same shape are possible:

>>> tstudent = TestStudent(ds1, ds7, name="comp",
...                        description="Comparison using Student's t-test")
>>> tstudent_res = tstudent.evaluate()
Traceback (most recent call last):
    ...
ValueError: Datasets to subtract do not have same shape

Multi-dimensional datasets are also allowed:

>>> ds8 = Dataset(np.array([[5.2, 5.3, 5.25], [5.4, 5.5, 5.2]]),
...               np.array([[0.2, 0.25, 0.1], [0.2, 0.3, 0.1]]))
>>> ds9 = Dataset(np.array([[5.1, 5.6, 5.2], [5.3, 5.2, 5.3]]),
...               np.array([[0.1, 0.3, 0.05], [0.4, 0.3, 0.2]]))
>>> ds8.shape
(2, 3)
>>> ds8.size
6
>>> tstudent = TestStudent(ds8, ds9, alpha=0.05, ndf=1000, name="comp",
...                        description="Comparison using Student's t-test")
>>> tstudent_res = tstudent.evaluate()
>>> bool(tstudent_res)
True
>>> print(np.array2string(tstudent_res.tstud[0],
...                       formatter={'float_kind':'{:.7f}'.format}))
[[0.4472136 -0.7682213 0.4472136]
 [0.2236068 0.7071068 -0.4472136]]
>>> print(np.array2string(tstudent_res.oracles()))
[[[ True  True  True]
  [ True  True  True]]]

Warning

If the errors are equal to 0, so the Student denominator is 0, AND the values are equal, so the numerator is also 0, the Student value is set to 0. In that case the test is assumed to succeed (boolean returning True).

>>> ds10 = Dataset(np.array([3.2, 0, 5]), np.array([0, 0.5, 0]))
>>> ds11 = Dataset(np.array([3.2, 0, 5.2]), np.array([0, 0.5, 0]))
>>> tstudent = TestStudent(ds10, ds11, name='zeros')
>>> tstudent_res = tstudent.evaluate()
>>> bool(tstudent_res)
False
>>> print(np.array2string(tstudent_res.tstud[0]))
[  0.   0. -inf]
>>> print(np.array2string(tstudent_res.oracles()))
[[ True  True False]]

class valjean.gavroche.stat_tests.student.TestResultStudent(test, tstud, pvalue=None)[source]

Result from Student’s t-test.

__init__(test, tstud, pvalue=None)[source]

Initialisation of TestResultStudent

Members are lists whose length corresponds to the number of datasets compared to the reference dataset.

Parameters:

test (TestStudent) – the TestStudent object
tstud (list (numpy.ndarray)) – Student’s t-test results
pvalue (list (numpy.generic) or list (list (numpy.generic))) – p-value or p-values depending on datasets, default is None

test_alpha(tstud)[source]

Test p-value or first kind error.

Parameters:: tstud (numpy.generic) – value of Student’s t-statistic to be used for comparison
Returns:: bool

oracles()[source]

Final test (if spectrum)

Returns:: list(bool)

__bool__()[source]

Has this test succeeded?

The policy for TestResultStudent is that the test is considered to fail if any of the p-values are below the given significance level. This means that a test on a Dataset having multiple bins will fail if any of the bins exhibits large fluctuations. You might want to use TestBonferroni or TestHolmBonferroni to deal with such cases.

If this test concerns multiple datasets, the test is considered to succeed if all the dataset individually pass the test against the reference.

test_pvalue()[source]

Result of the test by testing p-value.

Returns:: bool or numpy.ndarray of bool if ndf was given to TestStudent and datasets are numpy.ndarray

class valjean.gavroche.stat_tests.student.TestStudent(dsref, *datasets, name, description='', labels=None, alpha=0.01, ndf=None)[source]

Class to build the Student’s t-test.

__init__(dsref, *datasets, name, description='', labels=None, alpha=0.01, ndf=None)[source]

Initialisation of TestStudent

Parameters:

name (str) – local name of the test
description (str) – specific description of the test
labels (dict) – labels to be used for test classification in reports (for example category, input file name, type of result, …)
dsref (Dataset) – reference dataset
datasets (list (Dataset)) – list of datasets to be compared to reference dataset
alpha (float) – significance level, i.e. limit on the p-value (expected values are typically 0.01, 0.05), default is 0.01
ndf (int) – default is None, if given p-value will be calculated for ndf degrees of freedom (should correspond to number of batches), otherwise ndf assumed infinite, normal approximation

evaluate()[source]

Evaluate Student’s t-test method.

Returns:: TestResultStudent

static student_test(ds1, ds2)[source]

Compute Student’s t-test or Student distribution for the given datasets (static method).

Parameters:

ds1 (Dataset) – dataset 1
ds2 (Dataset) – dataset 2

Returns:

numpy.generic or numpy.ndarray depending on Dataset type

static pvalue(tstud, ndf)[source]

Calculation of the p-value (static method).

Parameters:

tstud (numpy.generic (float) or numpy.ndarray (float)) – Student’s t-test statistic
ndf (int or numpy.generic (int)) – number of degrees of freedom

Returns:

numpy.generic (float) or numpy.ndarray (float)

static student_threshold(alpha, ndf=None)[source]

Get threshold from probability (static method).

Parameters:

alpha (float or numpy.generic (float)) – required significance level ( $\alpha$ )
ndf (int or numpy.generic (int), default is None) – number of degrees of freedom

Returns:

numpy.generic (float)

The threshold is two-sided.

If number of degrees of freedom is given, the distribution used is the Student distribution corresponding to ndf. If not, we consider an infinite number of degrees of freedom. In that case, the Student distribution tends to a normal distribution.

data()[source]: Generator yielding objects supporting the buffer protocol that (as a whole) represent a serialized version of self.

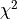`chi2` – $\chi^2$ test

In our case we’ll use the modified χ²-test widely used in physics for comparing histograms. This test is also available in the ROOT software. For further explanations a good desciption is provided by the documentation of ROOT’s Chi2Test() method on TH1 page or in this article by N. Gagunashvili.

The used formula is then:

$\chi^2_{obs} = \sum_{i=1}^p\frac{(x_{1i} - x_{2i})^2} {\sigma_{1i}^2 + \sigma_{2i}^2}$

where datasets (or distributions) 1 and 2 are compared, $x_i$ being the values and $\sigma_i$ being the error in each bin.

In our case only the ‘weighted’ case is implemented.

Statistical interpretation

The null hypothesis for the χ²-test is:

equal means in each bin
gaussian means in each bin (so normal distribution in each bin)
bins are independent

The interpretation of the test is based on the χ² value and on the p-value. Usually it is expected that the χ²/ndf should be close to 1 (ndf = number of degrees of freedom), see PDG, statistics chapter. The p-value can also be calculated from the probability density function of the χ² distribution, which is given by:

$pdf(x,k) = \frac{1}{2^{k/2}\Gamma(k/2)}x^{k/2-1}e^{-x/2}$

for $x > 0$ , $k$ the number of degrees of freedom and $\Gamma$ is Euler’s Gamma function [1].

The cumulative distribution function, $cdf$ , used to calculated the p-value is then:

$cdf(x,k) = \frac{\gamma(k/2,x/2)}{\Gamma(k/2)} = \int_{-\infty}^{x}pdf(t,k)dt$

where $\gamma$ is the lower incomplete gamma function [2].

It is equivalent to calculate the probability $P(x < \chi^2_{obs})$ which is equal to $1 - cdf(x,k)$ , so the integral from $x$ to $+\infty$ . This probability is the p-value.

If the p-value is lower than the define level (1%, 5% for example), the null hypothesis is rejected.

Possible biases can come from wrong estimation of uncertainties (underestimated for example or only statistical while a systematic one should be taken into account).

Code implementation

SciPy is used to calculate the p-value. The distribution scipy.stats.chi2 is imported as schi2` in order to name conflicts. The p-value is obtained with the sf method. It is directly compared with the significance level required by the user.

Warning

If some of your bins are not filled, if they are initialized to zero or if their error is zero, the χ² calculation will be wrong and probably give $\infty$ .

One option is proposed to remove these bins from the calculation, ignore_empty. The use of this option implies a reduction of the number of degrees of freedom by the number of removed bins (ndf = # bins). It has to be considered with caution, this does not make necessarly sense, depending on the user case.

Another option is to apply some rebinning in order to have no empty bins (what usually means re-running to get consistent uncertainties).

Examples of the test

Let’s consider a spectrum of 5 bins with their error and apply the χ²-test.

>>> from valjean.eponine.dataset import Dataset
>>> from valjean.gavroche.stat_tests.chi2 import TestChi2
>>> import numpy as np
>>> ds1 = Dataset(np.array([5.2, 5.3, 5.25, 5.4, 5.5]),
...               np.array([0.2, 0.25, 0.1, 0.2, 0.3]))
>>> ds2 = Dataset(np.array([5.1, 5.6, 5.2, 5.3, 5.2]),
...               np.array([0.1, 0.3, 0.05, 0.4, 0.3]))
>>> tchi2 = TestChi2(ds1, ds2, alpha=0.05, name="comp",
...                  description="Comparison using Chi2 test")
>>> tchi2_res = tchi2.evaluate()
>>> print(f'{tchi2_res.chi2_per_ndf[0]:.7f}')
0.3080328
>>> bool(tchi2_res)
True
>>> print(f'{tchi2_res.pvalue[0]:.7f}')
0.9083889

Test with empty bins

One “empty bin” at the same position in the 2 compared datasets prevents the test to work. An empty bin is defined as a bin with zero error. In Monte Carlo codes a zero error can happen for example when only one batch has been run, no variance can be calculated in that case (n-1 usually used with n the number of batches).

>>> ds3 = Dataset(np.array([5.2, 5.3, 5.25, 5.4, 5.5]),
...               np.array([0.2, 0.25, 0., 0.2, 0.3]))
>>> ds4 = Dataset(np.array([5.1, 5.6, 5.2, 5.3, 5.2]),
...               np.array([0.1, 0.3, 0., 0.4, 0.3]))
>>> tchi2 = TestChi2(ds3, ds4, alpha=0.05, name="comp",
...                  description="Comparison using Chi2 test")
>>> tchi2_res = tchi2.evaluate()
>>> tchi2_res.chi2
[inf]
>>> bool(tchi2_res)
False
>>> print(np.array2string(tchi2_res.test.nonzero_bins[0]))
[ True  True  True  True  True]
>>> tchi2_res.test.ndf[0]
5
>>> np.count_nonzero(ds4.error)
4

If the values are also at zero, we get a nan instead of an inf.

To get a χ² evaluation based on the non-empty bins, use the ignore_empty argument of the TestChi2. It recalculates the number of degrees of freedom removing the empty bins and only use the non-zero ones in the χ² calculation.

>>> tchi2 = TestChi2(ds3, ds4, alpha=0.05, ignore_empty=True,
...                  name="comp", description="Comparison using Chi2 test")
>>> tchi2_res = tchi2.evaluate()
>>> print(f'{tchi2_res.chi2[0]:.7f}')
1.3401639
>>> tchi2_res.test.ndf[0]
4
>>> tchi2_res.test.dsref.size
5
>>> print(np.array2string(tchi2_res.test.nonzero_bins[0]))
[ True  True False  True  True]
>>> print(f'{tchi2_res.chi2_per_ndf[0]:.7f}')
0.3350410
>>> bool(tchi2_res)
True

Test with multiple dimensions datasets

>>> ds5 = Dataset(np.array([[5.2, 5.3, 5.25], [5.4, 5.5, 5.2]]),
...               np.array([[0.2, 0.25, 0.1], [0.2, 0.3, 0.1]]))
>>> ds6 = Dataset(np.array([[5.1, 5.6, 5.2], [5.3, 5.2, 5.3]]),
...               np.array([[0.1, 0.3, 0.05], [0.4, 0.3, 0.2]]))
>>> ds5.shape
(2, 3)
>>> ds5.size
6
>>> tchi2 = TestChi2(ds5, ds6, alpha=0.05, name="comp",
...                  description="Comparison using Chi2 test")
>>> tchi2_res = tchi2.evaluate()
>>> print(f'{tchi2_res.chi2_per_ndf[0]:.7f}')
0.2900273
>>> bool(tchi2_res)
True
>>> print(f'{tchi2_res.pvalue[0]:.7f}')
0.9419786

And when we have at least one empty bin, using the ignore_empty argument:

>>> ds7 = Dataset(np.array([[5.2, 5.3, 5.25], [5.4, 5.5, 5.2]]),
...               np.array([[0.2, 0.25, 0.], [0.2, 0.3, 0.1]]))
>>> ds8 = Dataset(np.array([[5.1, 5.6, 5.2], [5.3, 5.2, 5.4]]),
...               np.array([[0.1, 0.3, 0.], [0.4, 0.3, 0.]]))
>>> ds7.shape
(2, 3)
>>> ds7.size
6
>>> tchi2 = TestChi2(ds7, ds8, alpha=0.05, ignore_empty=True,
...                  name="comp", description="Comparison using Chi2 test")
>>> tchi2_res = tchi2.evaluate()
>>> print(f'{tchi2_res.chi2[0]:.7f}')
5.3401639
>>> tchi2_res.test.ndf[0]
5
>>> tchi2_res.test.dsref.size
6
>>> print(np.array2string(tchi2_res.test.nonzero_bins[0]))
[[ True  True False]
 [ True  True  True]]
>>> print(f'{tchi2_res.chi2_per_ndf[0]:.7f}')
1.0680328
>>> bool(tchi2_res)
True

Note

A RuntimeWarning is emitted if zero bins are used during calculation.

Footnotes

class valjean.gavroche.stat_tests.chi2.TestResultChi2(test, chi2, pvalue)[source]

Result from the χ²-test.

__init__(test, chi2, pvalue)[source]

Construct a TestResultChi2 object.

Members are lists which length corresponds to the number of datasets compared to the reference dataset.

Parameters:

test (TestChi2) – the χ² test object
chi2 (list (numpy.generic (float))) – the value of the χ² statistic
pvalue (list (numpy.generic (float))) – the test p-value

oracles()[source]

Final test for the list of compared datasets.

Returns:: numpy.ndarray

property chi2_per_ndf

Calculate the χ² per number of degrees of freedom.

Returns:: χ²/ndf
Return type:: float

No parenthesis needed: this is a property.

class valjean.gavroche.stat_tests.chi2.TestChi2(dsref, *datasets, name, description='', labels=None, alpha=0.01, ignore_empty=False)[source]

Test class for χ², inheritate from Test.

__init__(dsref, *datasets, name, description='', labels=None, alpha=0.01, ignore_empty=False)[source]

Initialisation of TestChi2

Parameters:

name (str) – local name of the test
description (str) – specific description of the test
labels (dict) – labels to be used for test classification in reports (for example category, input file name, type of result, …)
dsref (Dataset) – reference dataset
datasets (list (Dataset)) – list of datasets to be compared to reference dataset
alpha (float) – probability to accept of not the test (p-value is expected greater), i.e. significance level
ignore_empty (bool) – if the array contains zero bins, the test can done not consider them if this option is True; otherwise it will probably fail as the array to sum will contain infinite terms. Default is False.

nonzero_bins: nonzero bins identification by True, False if zero (list (numpy.ndarray (bool)))

ndf: number of degrees of freedom (list (int))

static pvalue(chi2, ndf)[source]

Calculation of the p-value of the test.

Parameters:

chi2 (numpy.generic (float)) – observed χ²
ndf (int or numpy.generic (int)) – number of degrees of freedom

Returns:

numpy.generic (float)

static chi2_test(ds1, ds2, nonzero_bins=None)[source]

Compute the χ² value for the given datasets.

Parameters:

ds1 (Dataset) – first dataset
ds2 (Dataset) – second dataset
nonzero_bins (numpy.ndarray (bool) or None (default)) – optional argument, booleans array of the same size as ds1 and ds2 to identify zero bins and possibly avoid them (see below)

Returns:

χ² value

Return type:

numpy.generic (float)

It has to be noted that if in a bin the sum of the variances of the test and the reference dataset is zero (so both datasets bin has a zero error) the bin cannot be taken into account in the calculation of the sum as the ratio will be infinite. This is why they can be removed via the nonzero_bins argument at that step. This has another consequence: the number of degrees of freedom is consequently reduced by the number of bins removed.

evaluate()[source]

Evaluate χ² test method.

Return type:: TestResultChi2

data()[source]: Generator yielding objects supporting the buffer protocol that (as a whole) represent a serialized version of self.

`bonferroni` – Multiple hypothesis tests

In some cases we would like to interpret not only one test (like on a generic score in Tripoli-4) but multiple ones (in a spectrum case for example). Each individual test is supposed to be successful but in most of the case we can accept that some of them fail (in a given acceptance of course).

The Bonferroni correction and the Holm-Bonferroni method allow to treat such cases. See for example family-wise error rate Wikipedia webpage for more details on this kind of tests.

Here are implemented two tests based on comparison of the p-value from the chosen test and a significance level:

Bonferroni correction: all individual p-values are compared to the same significance level, depending on the number of tests;
Holm-Bonferroni method: p-values are first sorted then compared to different significance levels depending on number of tests and rank.

In both cases a first test is chosen, like Student test, to evaluate the individual hypothesis. The p-value of the test is calculated and used in the following tests. Like in other tests, we consider two-sided significance levels here.

The null hypothesis is that the p-value is higher than a given significance level, that depends on the overall required significance level, the number of tests considered and the chosen method (Bonferroni or Holm-Bonferroni).

Bonferroni correction

The Bonferroni correction is used for multiple comparisons. It is based on a weighted comparison to the significance level α.

If we have $m$ different tests (for example a spectrum with $m$ bins), the significance level α will be weighted by $m$ . This p-value of the $m$ tests will then be compared to that value. As a consequence, the null hypothesis will be rejected if

$p_k \leq \frac{\alpha}{m}$

The individual significance level is usually largely smaller than the required one and the sum of them obvioulsy give α.

Conclusion of the test depends on what we want:

it can be a simple True if all hypothesis are accepted;
it can be False if at least one null hypothesis was rejected;
we can also choose a level of acceptance, for example “it is fine if 1 % of the null hypothesis are rejected”

Per default, in our case the test is rejected if there is at least one null hypothesis rejected.

Holm-Bonferroni method

The Holm-Bonferroni method is a variation of the Bonferroni correction.

The p-value from the chosen test are first sorted from lower to higher value. Then each of them are compared to the significance level weighted by $m - k + 1$ with $m$ the number of tests and $k$ the rank (starting at 1). The null hypothesis is rejected if

$p_k \leq \frac{\alpha}{m - k + 1}.$

The test can be stopped at the first $k$ accepting the null hypothesis.

This test is quite conservative. It can be possible to get the proportion of accepted and rejected hypothesis, like in the Bonferroni correction case.

Code implementation

In both cases, the test is initiliazed with another test, a Student test for example. This test can be evaluated inside the new test evaluate method or outside of it. Only examples with the full structure will be shown here.

TestResults are returned as False if one null hypothesis is rejected. Access to the initial test is still provided.

Examples

Let’s do the usual imports then use the quick example from Student test, with the p-value calculation:

>>> import numpy as np
>>> from valjean.eponine.dataset import Dataset
>>> from valjean.gavroche.stat_tests.student import TestStudent
>>> from valjean.gavroche.stat_tests.bonferroni import TestBonferroni
>>> from valjean.gavroche.stat_tests.bonferroni import TestHolmBonferroni

Successful test with Bonferroni correction and Holm-Bonferroni method

>>> ds1 = Dataset(np.array([5.2, 5.3, 5.25, 5.4, 5.5]),
...               np.array([0.2, 0.25, 0.1, 0.2, 0.3]))
>>> ds2 = Dataset(np.array([5.1, 5.6, 5.2, 5.3, 5.2]),
...               np.array([0.1, 0.3, 0.05, 0.4, 0.3]))
>>> tstudent_12 = TestStudent(ds1, ds2, name="comp",
...                           description="Comparison using Student test",
...                           alpha=0.05, ndf=1000)

>>> tbonf = TestBonferroni(name="bonf", description="Bonferroni correction",
...                        test=tstudent_12, alpha=0.05)
>>> tbonf.ntests
5
>>> tbonf.ntests == ds1.size
True
>>> tbonf.bonf_signi_level
0.005
>>> tbonf_res = tbonf.evaluate()
>>> bool(tbonf_res)
True
>>> tbonf_res.nb_rejected
[0]

>>> tholmbonf = TestHolmBonferroni(name="holm-bonf",
...                                description="Holm-Bonferroni method",
...                                test=tstudent_12, alpha=0.05)
>>> tholmbonf.alpha  # alpha is two-sided
0.025
>>> thb_res = tholmbonf.evaluate()
>>> bool(thb_res)
True
>>> thb_res.nb_rejected
[0]

Failing test with Bonferroni correction and Holm-Bonferroni method

>>> ds3 = Dataset(np.array([5.1, 5.9, 5.8, 5.3, 4.6]),
...               np.array([0.1, 0.1, 0.05, 0.4, 0.12]))
>>> tstudent_13 = TestStudent(ds1, ds3, name="comp",
...                           description="Comparison using Student test",
...                           alpha=0.05, ndf=1000)

>>> tbonf = TestBonferroni(name="bonf", description="Bonferroni correction",
...                        test=tstudent_13, alpha=0.05)
>>> tbonf.ntests
5
>>> tbonf.bonf_signi_level
0.005
>>> tbonf_res = tbonf.evaluate()
>>> bool(tbonf_res)
False
>>> tbonf_res.nb_rejected
[1]
>>> tbonf_res.rejected_proportion  # in percentage
[20.0]

>>> tholmbonf = TestHolmBonferroni(name="holm-bonf",
...                                description="Holm-Bonferroni method",
...                                test=tstudent_13, alpha=0.05)
>>> tholmbonf.alpha  # alpha is two-sided
0.025
>>> thb_res = tholmbonf.evaluate()
>>> bool(thb_res)
False
>>> thb_res.nb_rejected
[2]
>>> thb_res.rejected_proportion  # in percentage
[40.0]

For an easier comparison, p-values, associated significance levels and the corresponding result from the test (rejection or not) can be printed. The sorting order is also given for the Holm-Bonferroni method.

>>> it = np.nditer([thb_res.first_test_res.pvalue,
...                 tbonf.bonf_signi_level, tbonf_res.rejected_null_hyp,
...                 thb_res.sort_ordering, thb_res.alphas_i,
...                 thb_res.rejected_null_hyp],
...                flags=['multi_index'])
>>> while not it.finished:
...     if it.iterindex == 0:
...         print("index  | pvalue(B) |   α(B)    |  reject B | order(HB) |"
...               f"   α(HB)   | reject HB\n{'-':->77}")
...     print(f"{it.multi_index} | {it[0]:.3e} | {it[1]:.3e} | {it[2]!s:^9} | "
...           f"{it[3]:^7}   | {it[4]:.3e} |   {it[5]!s:<}")
...     _ = it.iternext()
index  | pvalue(B) |   α(B)    |  reject B | order(HB) |   α(HB)   | reject HB
-----------------------------------------------------------------------------
(0, 0) | 6.548e-01 | 5.000e-03 |   False   |    3      | 1.250e-02 |   False
(0, 1) | 2.608e-02 | 5.000e-03 |   False   |    2      | 8.333e-03 |   False
(0, 2) | 1.015e-06 | 5.000e-03 |   True    |    0      | 5.000e-03 |   True
(0, 3) | 8.231e-01 | 5.000e-03 |   False   |    4      | 2.500e-02 |   False
(0, 4) | 5.447e-03 | 5.000e-03 |   False   |    1      | 6.250e-03 |   True

The first index corresponds to the index of the compared dataset in the datasets container in the input test (compared to dsref).

The Holm-Bonferroni test is uniformly more powerful than the Bonferroni test. In this particular case, Holm-Bonferroni is able to reject an additional null hypothesis with respect to plain Bonferroni.

Tests with multi-dimension datasets

>>> ds4 = Dataset(np.array([[5.2, 5.3, 5.25], [5.4, 5.5, 5.2]]),
...               np.array([[0.2, 0.25, 0.1], [0.2, 0.3, 0.25]]))
>>> ds5 = Dataset(np.array([[5.1, 5.9, 5.8], [5.3, 4.7, 5.5]]),
...               np.array([[0.1, 0.1, 0.05], [0.4, 0.05, 0.2]]))
>>> ds4.shape
(2, 3)
>>> ds4.size
6
>>> tstudent_45 = TestStudent(ds4, ds5, name="comp",
...                           description="Comparison using Student test",
...                           alpha=0.05, ndf=1000)

>>> tbonf = TestBonferroni(name="bonf", description="Bonferroni correction",
...                        test=tstudent_45, alpha=0.05)
>>> tbonf.ntests
6
>>> print(f'{tbonf.bonf_signi_level:.6f}')
0.004167
>>> tbonf_res = tbonf.evaluate()
>>> bool(tbonf_res)
False
>>> tbonf_res.nb_rejected
[1]
>>> print(f'{tbonf_res.rejected_proportion[0]:.3f} %')
16.667 %

>>> tholmbonf = TestHolmBonferroni(name="holm-bonf",
...                                description="Holm-Bonferroni method",
...                                test=tstudent_45, alpha=0.05)
>>> thb_res = tholmbonf.evaluate()
>>> tholmbonf.alpha
0.025
>>> bool(thb_res)
False
>>> thb_res.nb_rejected
[1]
>>> print(f'{thb_res.rejected_proportion[0]:.3f} %')
16.667 %

The detailed comparison also works for multi-dimensions arrays:

>>> it = np.nditer([thb_res.first_test_res.pvalue, tbonf.bonf_signi_level,
...                 tbonf_res.rejected_null_hyp, thb_res.sort_ordering,
...                 thb_res.alphas_i, thb_res.rejected_null_hyp],
...                flags=['multi_index'])
>>> while not it.finished:
...     if it.iterindex == 0:
...         print("index     | pvalue(B) |   α(B)   | reject B | order(HB) |"
...               f"   α(HB)  | reject HB\n{'-':->79}")
...     print(f"{it.multi_index} |  {it[0]:.2e} | {it[1]:.2e} | {it[2]!s:^7}  "
...           f"| {it[3]:^7}   | {it[4]:.2e} |   {it[5]!s:<}")
...     _ = it.iternext()
index     | pvalue(B) |   α(B)   | reject B | order(HB) |   α(HB)  | reject HB
-------------------------------------------------------------------------------
(0, 0, 0) |  6.55e-01 | 4.17e-03 |  False   |    4      | 1.25e-02 |   False
(0, 0, 1) |  2.61e-02 | 4.17e-03 |  False   |    2      | 6.25e-03 |   False
(0, 0, 2) |  1.01e-06 | 4.17e-03 |  True    |    0      | 4.17e-03 |   True
(0, 1, 0) |  8.23e-01 | 4.17e-03 |  False   |    5      | 2.50e-02 |   False
(0, 1, 1) |  8.66e-03 | 4.17e-03 |  False   |    1      | 5.00e-03 |   False
(0, 1, 2) |  3.49e-01 | 4.17e-03 |  False   |    3      | 8.33e-03 |   False

The first index corresponds to the index of the compared dataset in the datasets container in the input test (compared to dsref). The next ones correspond to the shape of the arrays.

The sorting order for Holm-Bonferroni considers all elements as equivalent (not done per dimension).

class valjean.gavroche.stat_tests.bonferroni.TestResultBonferroni(test, first_test_res, rejected_null_hyp)[source]

Test result from Bonferroni correction.

The test returns True if the test is successful (null hypothesis was accepted) and False if it is rejected.

__init__(test, first_test_res, rejected_null_hyp)[source]

Initialisation of TestResultBonferroni

Parameters:

test (TestBonferroni) – the used Bonferroni test
first_test_res (TestResult child class) – the test result used to obtain the p-values
reject_hyp (numpy.ndarray (bool)) – rejection of the null hypothesis for all bins

oracles()[source]

Final test (on list of tests, espacially in case of mulitple tests on common reference).

Returns:: list(bool)

property nb_rejected

Number of rejected null hypothesis according Holm-Bonferroni test.

Returns:: list(int) or list (numpy.generic (int))

property rejected_proportion

Rejected proportion in percentage.

Returns:: list (numpy.generic (float))

class valjean.gavroche.stat_tests.bonferroni.TestBonferroni(*, name, description='', labels=None, test, alpha=0.01)[source]

Bonferroni correction for multiple tests of the same hypothesis.

__init__(*, name, description='', labels=None, test, alpha=0.01)[source]

Initialisation of TestBonferroni.

Parameters:

name (str) – local name of the test
description (str) – specific description of the test
labels (dict) – labels to be used for test classification in reports (for example category, input file name, type of result, …)
test (valjean.gavroche.test.Test child class) – test from which pvalues will be extracted
alpha (float) – required significance level

The significance level is considered two-sided here, so divide by 2. It is the significance level for the whole test.

property ntests: Returns the number of hypotheses to test, i.e. number of bins here.

static bonferroni_correction(pvalues, bonf_signi_level)[source]

Bonferroni correction.

Parameters:

pvalues (numpy.ndarray (float)) – p-values from the original test
bonf_signi_level (float) – significance level for each test (α weighted by the number of tests)

Returns:

numpy.ndarray (bool)

Compares the p-value to the “Bonferroni significance level”:

if lower, null hypothesis is rejected for the bin
if higher, null hypothesis is accepted for the bin.

evaluate()[source]

Evaluate the Bonferroni correction.

Returns:: TestResultBonferroni

data()[source]: Generator yielding objects supporting the buffer protocol that (as a whole) represent a serialized version of self.

class valjean.gavroche.stat_tests.bonferroni.TestResultHolmBonferroni(test, first_test_res, alphas_i, rejected_null_hyp)[source]

Result from the Holm-Bonferroni method.

__init__(test, first_test_res, alphas_i, rejected_null_hyp)[source]

Initialisation of TestResultHolmBonferroni

Parameters:

test (TestHolmBonferroni) – the used Holm-Bonferroni test
first_test_res (TestResult child class) – the test result used to obtain the p-values
sorted_indices (numpy.generic (int)) – indices of the p-values sorted to get p-values in increasing order
alphas_i (numpy.ndarray (float)) – significance levels for sorted pvalues
rejected_hyp (numpy.ndarray (bool)) – rejection of the null hypothesis for all bins

oracles()[source]

Final test (on list of tests, espacially in case of mulitple tests on common reference).

Returns:: list(bool)

property nb_rejected

Number of rejected null hypothesis according Holm-Bonferroni test.

Returns:: list(int) or list (numpy.generic (int))

property rejected_proportion

Rejected proportion in percentage.

Returns:: list (numpy.generic (float))

property sort_ordering

Get the sorted pvalues.

Returns:: list (numpy.generic (int))

class valjean.gavroche.stat_tests.bonferroni.TestHolmBonferroni(*, name, description='', labels=None, test, alpha=0.01)[source]

Holm-Bonferroni method for multiple tests of the same hypothesis.

__init__(*, name, description='', labels=None, test, alpha=0.01)[source]

Initialisation of TestHolmBonferroni.

Parameters:

name (str) – local name of the test
description (str) – specific description of the test
labels (dict) – labels to be used for test classification in reports (for example category, jdd name, type of result, …)
test (valjean.gavroche.test.Test child class) – test from which pvalues will be extracted
alpha (float) – significance level

The significance level is also considered two-sided here, so divide by 2. This is the overall significance level.

property ntests: Returns the number of hypotheses to test, i.e. number of bins here.

static holm_bonferroni_method(pvalues, alpha)[source]

Holm-Bonferroni method.

Parameters:

pvalues (numpy.ndarray) – array of pvalues
alpha (float) – significance level chosen for the Holm-Bonferroni method

Returns:

sorted indices, array of the bins significance level, array of rejection of the null hypothesis

evaluate()[source]

Evaluation of the used test and of the Holm-Bonferroni method.

Returns:: TestResultHolmBonferroni

data()[source]: Generator yielding objects supporting the buffer protocol that (as a whole) represent a serialized version of self.

stat_tests – Statistical tests for datasets comparisons

Introduction

Modules

student — Student’s t-test

Test interpretation

Code implementation

Examples

chi2 – test

Statistical interpretation

Code implementation

Examples of the test

Test with empty bins

Test with multiple dimensions datasets

bonferroni – Multiple hypothesis tests

Bonferroni correction

Holm-Bonferroni method

Code implementation

Examples

Successful test with Bonferroni correction and Holm-Bonferroni method

Failing test with Bonferroni correction and Holm-Bonferroni method

Tests with multi-dimension datasets

`stat_tests` – Statistical tests for datasets comparisons

`student` — Student’s t-test

`chi2` – $\chi^2$ test

`bonferroni` – Multiple hypothesis tests